事例１：人間オペレータによる倒立棒の安定化制御

図１は、人間とロボットにおける倒立棒の安定化制御の例を示します。

図1-aは、ごく普通の体格をした山形県の鈴木みなとさんという女性が米俵を5俵（300キロ）背負って平然と歩いている写真です。ものを担ぐといった単純に見える動きでも、上手に担げば、普通の人の何倍もの重さを担げることを示しています。
	図1-a　鈴木みなとさん　山形県酒田市藤食倉庫、怪力法若木竹丸著

図1-bは、秋田竿燈まつり2008年のポスターです。竿燈全体を稲穂に、連なる提灯を米俵に見立て、額・腰・肩などにのせ、豊作を祈ります。
	図1-b　2008年秋田竿燈まつり

図1-cは、腕を大きく振らない、足で強く蹴らない高橋尚子選手の「忍者走り」です。
	図1-c　高橋尚子の走り（さかいやスポーツ提供)

図1-dは、江戸－仙台間300 kmを１日で走ったといわれる伝説の飛脚にちなんで「源兵衛」と名付けた二足歩行ロボットの転倒力を利用した「ナンバ走り・飛脚走り」です。
	図1-d　二足歩行ロボット源兵衛の走り

図２は人間オペレータによる台車上の倒立棒の安定化制御の例です。手で台車を左右に移動させて倒立棒が倒れないように操作します。

図２　人間による台車上の倒立棒の安定化制御

図３はその習熟過程を示します。垂直に立つ（静止しているときは垂直に立たないと転倒する）という意味ではなく、転倒しないという意味の安定化制御が練習により可能になります。

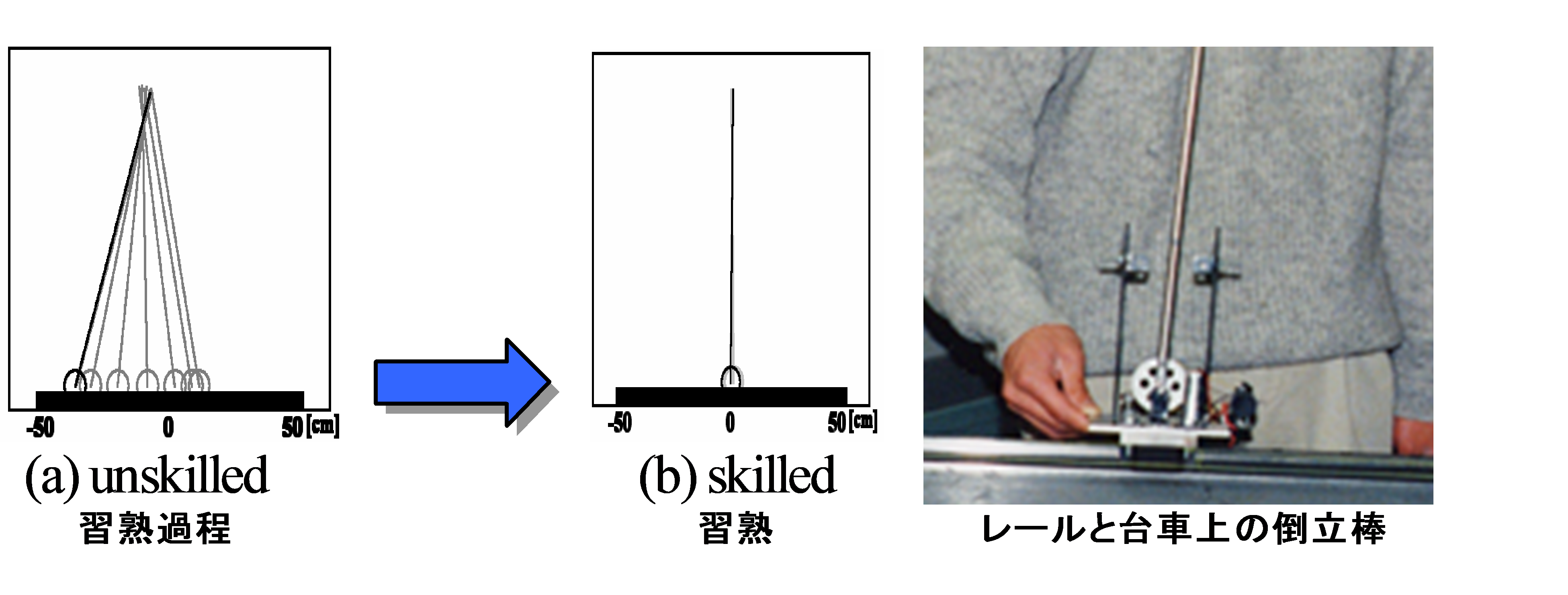図３　人間オペレータによる倒立棒の安定化制御における習熟過程

従来の一般的な機械制御では、目標値である垂直位置との差を最小にするために、倒立棒を常に垂直に立てようとしますが、人間は倒立棒を倒さない範囲の有限振幅に目標値との差を保つような制御をします。四六時中制御するのではなく、倒れる心配がない瞬間は手を抜きます。
倒立棒はほとんど垂直には立っておらず、常に揺れています。垂直に立っているように見える熟練者の場合でも、実は、常に微妙に揺れているのです。

著名な生態心理学者・ギブソンは、「ヒトの立つことは、止まることではなく、倒れないための「不安定幅」の持続であり、「姿勢」の止まらないという性質が身体に動きをもたらす。」と言っています。鋭い指摘です。

この発想は、柔軟でロバスト（頑健）な直立二足歩行ロボットの自在の動きに展開することができます。

図４は、垂直への目標値追従型の（常に垂直状態に近づけようと制御する）オペレータは習熟しにくく、初期の段階において大きく傾かせて大胆な切り替え操作をするオペレータの方が習熟しやすいことを示しています。
大きく傾かせながら大胆に操作するほうが、身体が棒の性質を同定しやすいのだと考えられます。
二足歩行ロボットで一般的に用いられるZMP（ゼロ・モーメント・ポイント）制御（転倒モーメントをゼロにする）が俊敏自在の大胆な動きができないのは、目標値追従型だからです。

「小成は大成を妨げる最大の要素である」という古武術研究者・甲野善紀先生の持論は、ロボットの世界でも同じです。

図４　目標値に追従する従来型ZMP（ゼロ・モーメント・ポイント）制御に似た安定化挙動の例（スティックピクチャー、オペレータNR01）試行開始からほぼ垂直に近く制御されているが、10秒後に転倒している（ストッパに衝突）。

人間オペレータによる台車上の倒立棒の安定化制御において、実測の時系列データおよびニューラル制御器・ファジィ制御器により同定した結果から、人間オペレータの安定化挙動には、
(1) カオス性（最大リアプノフ数が正）と無秩序さの程度（エントロピーの割合）が大きいこと、
(2) 試行回数を重ねると次第に運動の自由度が増し、無秩序さの程度が低減すること、
(3) ファジィ制御器は習熟の初期段階の同定に適しており、ニューロ制御器は習熟のレベルが高い段階の同定に適していること、
などが明らかになりました。

将来、ファジィ制御、ニューラル制御、それらのハイブリッド制御への展開などにより、生体系の運動の同定や生き物のような運動の生成が可能になれば、多量のエネルギーや複雑なプロセスを使うことなく、少ない手間で自発的にユニークな制御をするシステムの可能性が期待できます。

図５(a)と(b)は、古武術研究者・甲野善紀先生によるパテェシェ（菓子職人）の混ぜ方の提示例であり、(a) 身体全体の関節を使った自由度の高い動き（疲れにくい）、(b) 腕の動きが目立つ自由度の低い動き（疲れやすい）を示します。

図5-a　自由度の大きい動き（疲れにくい）

図5-b 自由度の少ない動き（疲れやすい）

図５古武術研究者・甲野善紀によるパテェシェ（菓子職人）の混ぜ方の提示例

図６(a)、 (b) は、模型の鉄棒人形が、電磁石と永久磁石による土台と足裏の間の反発により、大きい初期角度と初期角速度を与えられて大車輪を行うときのほぼ1回転のコマ写真です。（2自由度・二重振子の強制振動の実測例）

強制力（磁石の反発力）が一定であるのに、周期は(a)では0。51秒、(b)では0。70秒であり、振幅も毎回微妙に異なり、周期性と無秩序さが同居する複雑系（カオス挙動）であることを示しています。

春夏秋冬、朝昼晩は繰り返しても、去年の夏と今年の夏は同じではなく、我々の住む世界も、半ば規則的、半ば不規則な複雑系の世界だから、何が起こるかわからないということになります。

振子の周期も、振子の長さだけで決まると高校物理では教えられますが、振れる角度（振幅）が小さい場合に限って周期はほぼ一定ということであって、実際は、周期は振幅によっても変わるので、大振幅になると解析できなくなります（非線形の世界）。

鉄棒の大車輪運動の難しさが想像できます。

(a) 回転周期： 0.51 s （秒）

(b) 回転周期：0.70s （秒）

図６模型の鉄棒人形の大車輪（二重振り子の強制振動）における複雑系（周期性と無秩序さが同居）