テニスラケットの科学(586) :スピン量と打球速度はインパクト(1000分の3~5秒)で決まる⑤ :打球速度とスピンの生成原理(例2) :反発力係数 e が打球速度(速さと方向)とスピン量を変える! :ストリング面のスイート・スポット(e=0.4)で打撃した場合と先端側(e=0.2)で打撃した場合の打球の速さと方向とスピン量の比較
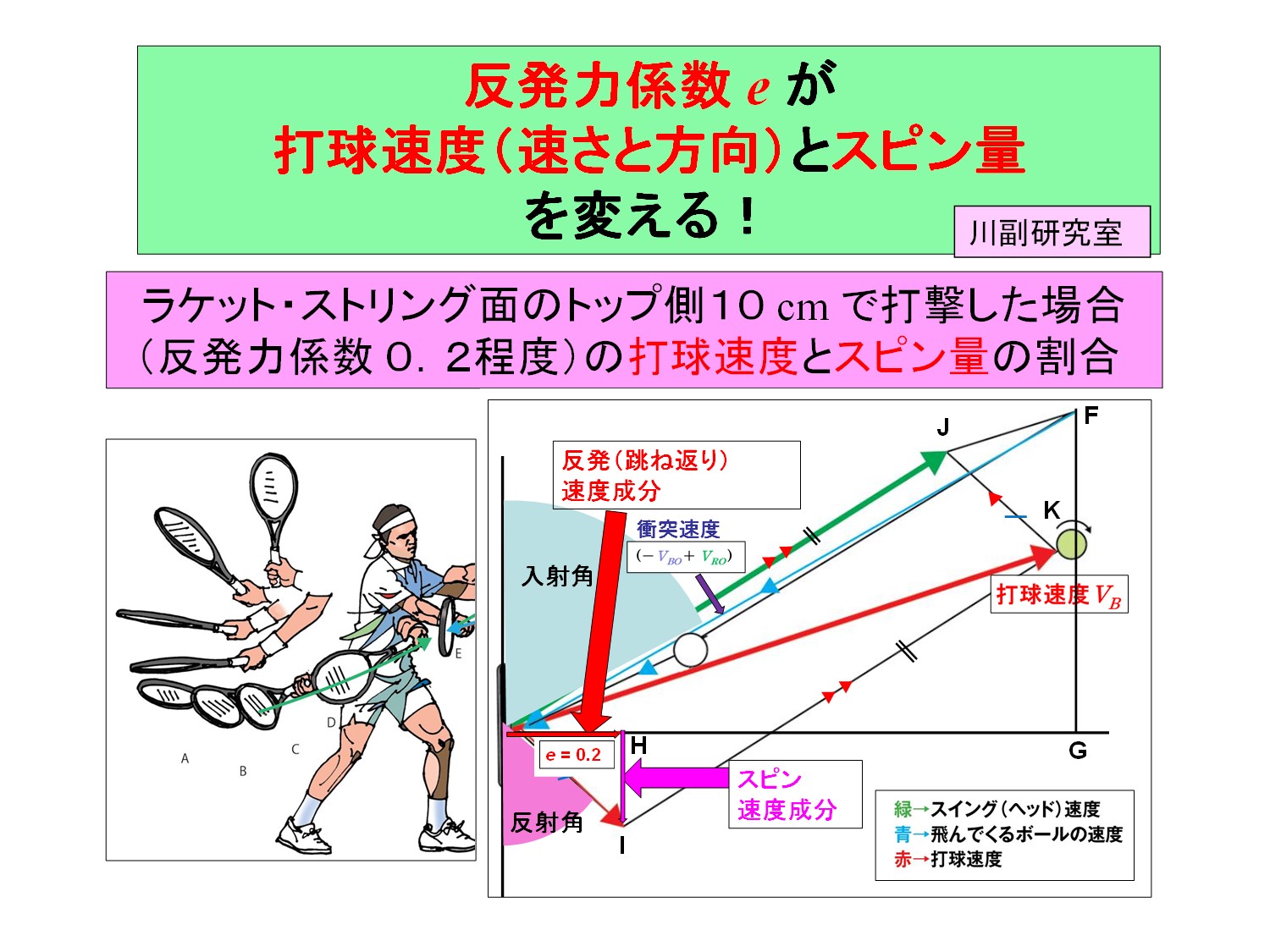
● 図1は、フェデラー選手をモデルとして、高速度カメラで実打を撮影した映像に基づいてイラスト化したものです。
図―1
フォアハンド・トップスピンのインパクト後の打球速度、方向、スピン量(回転角速度)が、
「インパクトにおける
①スイングの速度
②スイングの方向
③ ラケット面の傾き」
という三つの要素によって、どのように発現するかを示したものです。
・ インパクト直前と直後のボールの挙動の変化には、ボール・ラケット間の反発特性や摩擦特性など、複雑な要素が関係するので解析は難しいのですが、これは実際にボールを打ったときの映像の連続写真に基づいています。
・ この実測データから、反発力係数が約0.2、すなわち、ストリング面の中心から先端側10センチのあたりで打撃したことが推測されます。
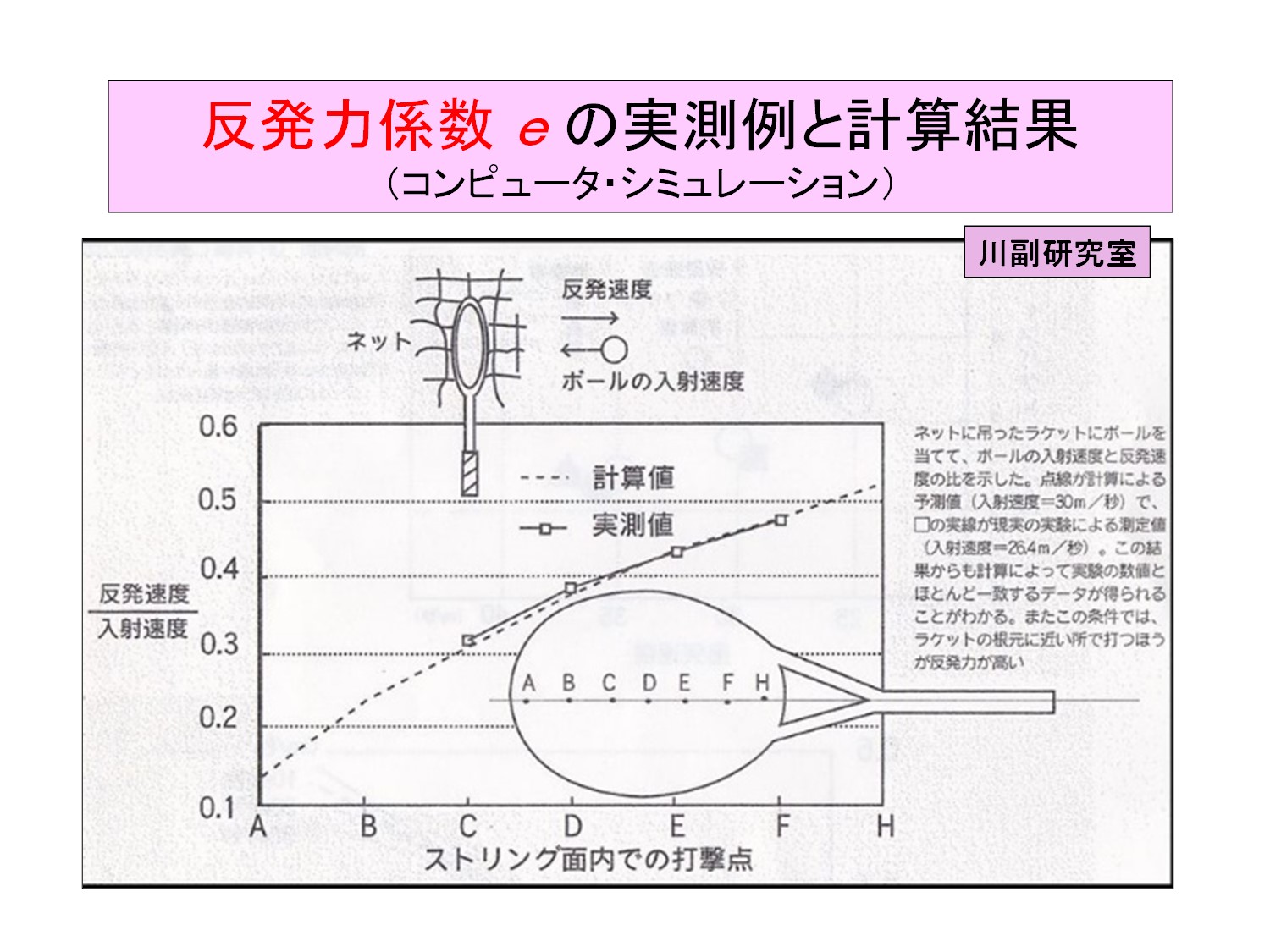
● 図2は、反発力係数 e の実測例と計算結果(コンピュータ・シミュレーション)を参考までに示しました。
図―2
プレーヤのスイング・モデルとラケットから構成される系の反発力係数の値も、宙づりラケットの反発力係数の値もほとんど違いがありません。
その理由や実験結果については、別稿で紹介させていただきます。
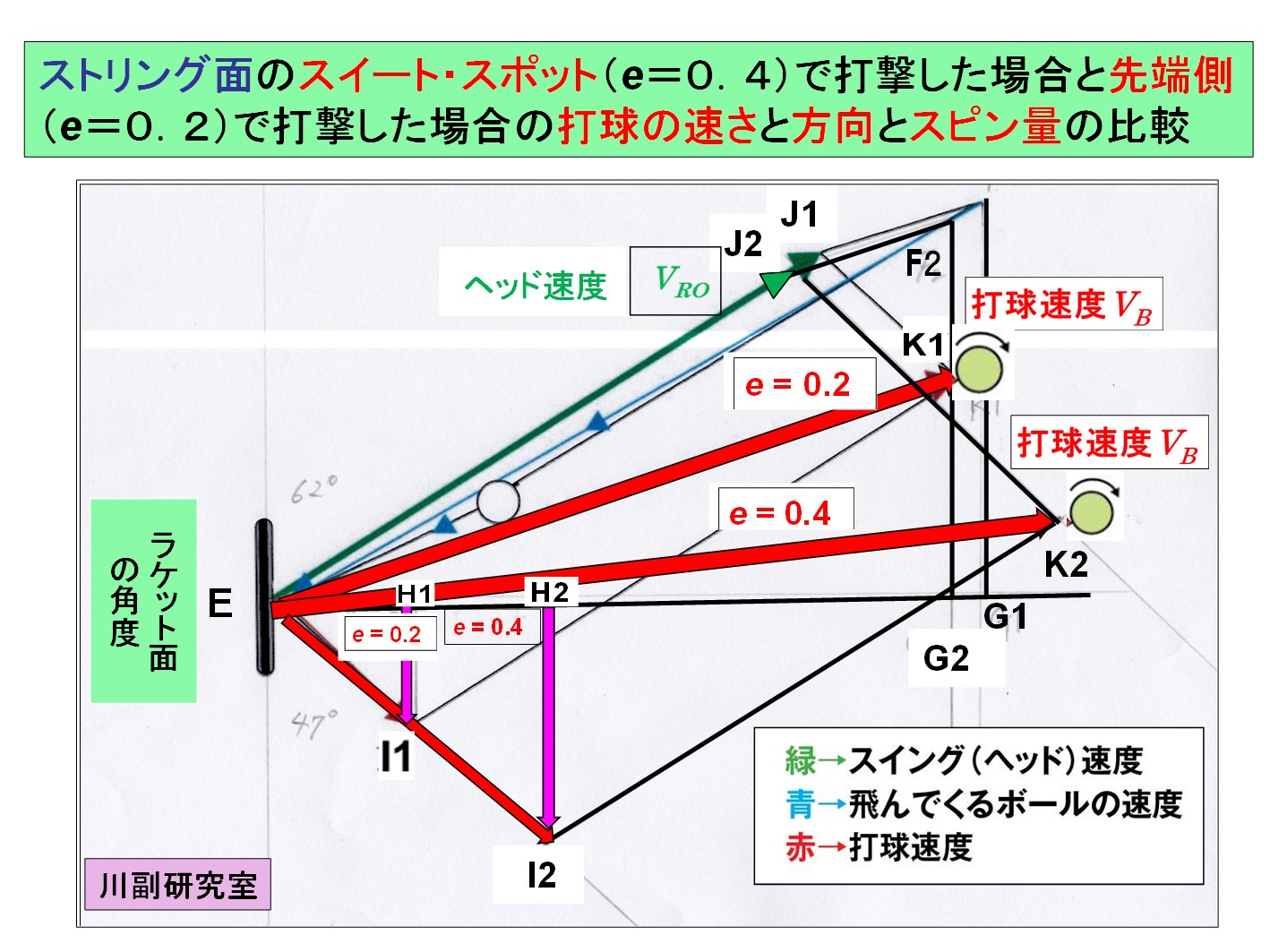
● 図3は、ラケット面に対するボールの入射角(飛来するボール速度とラケットヘッド速度のベクトル和)と反射角の関係が同一として、ストリング面のスイート・スポット(e=0.4)で打撃した場合と先端側(e=0.2)で打撃した場合の打球の速さと方向とスピン量の比較したものです。
図―3
・ 打球速度は、スイート・スポット(e=0.4)で打撃した場合は、先端側(e=0.2)で打撃した場合と比べて、ヘッド速度は 5 % ほど小さくなりますが、打球速度は 4 % ほど大きく、スピン量は2倍ほどになっていることが推測されます。
・ インパクトにおけるラケットヘッドのスイング軌道は、上方へ33度になっていますが、ストリング面の先端側に比べて2倍ほど反発力の大きいスイートスポットでハードヒットしても、スピン量が大きいので、コートに収まることが理解できます。
・ スピン量が大きいほど、インパクトにおけるスイング・ヘッド速度の軌道と打球速度の軌道の角度の違いが大きくなるので、ハードヒットしてもコートに収まりやすくても、精密なボール・コントロールは難しいことを示しているかもしれませんね!
(続く)
(参考資料)
・ テニスラケットの科学(583)
:スピン量と打球速度はインパクト(1000分の3~5秒)で決まる➃
:打球速度とスピンの生成原理(例)
:ストリング面のスイート・スポット(反発力係数0.4程度)でトップスピン打撃した場合(ストリング面の先端側での打撃との比較)
https://kawazoe-lab.com/tennis_racket/science-of-tennis-racket-583/
・ テニスラケットの科学(582)
:スピン量と打球速度はインパクト(1000分の3~5秒)で決まる➂
:打球速度とスピンが生まれるインパクトの原理
:(インパクトにおける)飛来するボール速度、ラケット・ヘッド速度、ラケット面の角度、反発力係数と打球速度、スピン量の関係
https://kawazoe-lab.com/tennis_racket/science-of-tennis-racket-582/
・ テニスラケットの科学(581)
:テニスラケットの科学(460)の補足2
:ラケットの性能とプレーヤのパフォーマンスの関係①
:Q&Aより
https://kawazoe-lab.com/tennis_racket/science-of-tennis-racket-581/
・ テニスラケットの科学(8)
:グリップ自由の(手の支えのない)ラケットにボールを衝突させたときの各打点の反発力係数 (実測値とシミュレーション計算値)
https://kawazoe-lab.com/tennis_racket/science-of-tennis-racket-8/
